Nodes and Edges
In the previous page, I said graph theory boils down to places to go, and ways to get there. Let's have another look at the definition I used earlier.
A graph refers to a collection of nodes and a collection of edges that connect pairs of nodes.
Nodes: Places to be
Edges: Ways to get there
In the Königsberg example, the land masses and islands are nodes, and the bridges are edges.
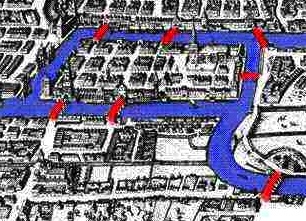
Traditional map
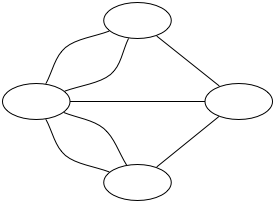
Euler's version
- About This Site
- Git Makes More Sense When You Understand X
- Example 1: Kent Beck
- Example 2: Git for Ages 4 and Up
- Example 3: Homeomorphic Endofunctors
- Example 4: LSD and Chainsaws
- The Internet Talks Back!
- Graph Theory
- Seven Bridges of Königsberg
- Places To Go, and Ways to Get There
- Nodes and Edges ←HEAD
- Attaching Labels to Nodes
- Attaching Labels to Edges
- Directed Versus Undirected Graphs
- Reachability
- Graphs and Git
- Visualizing Your Git Repository
- References
- The Reference Reference
- Making Sense of the Display
- Garbage Collection
- Experimenting With Git
- References Make Commits Reachable
- My Humble Beginnings
- Branches as Savepoints
- Use Your Targeting Computer, Luke
- Testing Out Merges
- Rebase From the Ground Up
- Cherry-Picking Explained
- Using 'git cherry-pick' to Simulate 'git rebase'
- A Helpful Mnemonic for 'git rebase' Arguments
- The End
